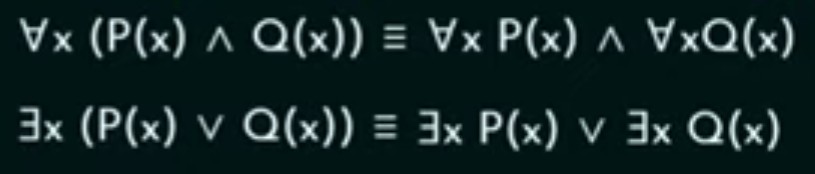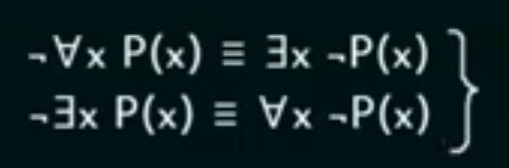2022-02-15 00:00:00 +0000 - Written By Omprakash
What is a Proposition?
Any statement that is either true or false, is termed as proposition.
There are two laws regarding proposition as follows:
-
Law of excluded middle
This law states that a proposition is required to be either true or false but not both.
-
Law of contradiction
True = not False False = not True -
Types of proposition:
-
Atomic Proposition : Any proposition which cannot be further divded is termed as atomic proposition.
-
Compound Proposition : One or more atomic proposition combined to form a compound proposition using connectors/operators (i.e ~, ^, v, ->, <->).
-
Note:- Both atomic and compound Proposition's are generally termed as Premises. -
Tautology: A propositional function which is true in every possible case. A tautology is also termed as Valid statement.
-
Contradiction : A propositional function which is false in every possible case.
-
Contingency : A propositional function which is some time true and sometime false.
-
Satisfiability
A statement or a propsoition is said to be satisfiable if its truth table has atleast one true value, otherwise statement is unsatisfiable.
Clearly, Tautology and Contingency are satisfiable whereas Contradiction is unsatisfiable.
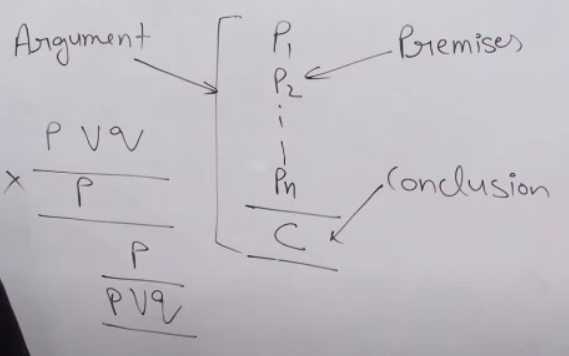
What is Argument?
Collection of Premises on the basis of which we derive a conclusion is termed as Argument.
Connectors / Operators
- Negation (~) : It is a NOT of digital electronics.
| P | ~P |
|---|---|
| True | False |
| False | True |
- Disjunction (v) : It is a OR of digital electronics.
| P | Q | P v Q |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| False | False | False |
- Conjunction (^) : It is AND of Digital Electronics
| P | Q | P ^ Q |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
-
Implication (->) : It is also an binary operator. P -> Q, is read as If P then Q.
- With truth table as follows:
| P | Q | P -> Q |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | True |
| False | False | True |
-
P -> Q = ~p v Q | If P then Q is equal to Not P OR Q -
Bidirectional operator (<->) :
- If sigifies if and only if (i.e iff)
- Work as Ex-NOR of digital electronics
P Q P <-> Q True True True True False Flase False True False False False True
Precedence of Operators
| Operators | Name | Precedence |
|---|---|---|
| ~ | Negation | 1 |
| ^ | Conjunction | 2 |
| v | Disjunctin | 3 |
| -> | Implication | 4 |
| <-> | Biconditional | 5 |
Converse, Inverse & Contrapositive
| Statement | If p, then q. | If two angles are Congurent, then they have same measure. |
| Converse | If q, then P. | If two angles have same measure, then they are congurent. |
| Inverse | If not p, then not q. | If two angles are not Congurent, then they don't have same measure. |
| Contrapositive | If not q, then not p | If two angles don't have same measure, then they are not congurent. |
Quantifiers
First we have to understand the concept of Predicates. One of the downside of propositonal-logic is that we cannot restrict the domain of the subject, predicate’s help us to do so.
Predicate are wriitten as P(x), where P is the logic and x is the subject.
Predicates are used alongside quantifiers to express the extent to which a predicate is true over a range(domain) of elements.
There are two types of quantifiers:
- Universal Quantifier
- Existential Quantifier
Some Properties of Quantifiers